Build tree from traversals
This post is inspired by leetcode 106 and the excellent solution breakdown by leetcode-master.
Problem
Given the inorder and postorder traversal results of a tree (assuming tree nodes are unique), build the tree. Example:
inorder: [9, 3, 15, 20, 7]
postorder: [9, 15, 7, 20, 3]
tree: 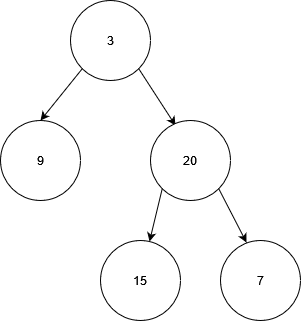
Strategy
Knowing that inorder traversal is left subtree -> middle node -> right subtree and postorder traversal is left subtree -> right subtree -> middle node, we will be able to always identify the folowing:
-
middle node: which is always the last element of the postorder array.
-
left subtree: given the middle node, we will be able to search for it in the inorder array, what is left to it must be elements of the left subtree.
-
right subtree: similarly, what is right to the middle node must be elements of the right subtree.
In our example, middle node = {3}, left subtree = {9} and right subtree = {20, 15, 7}. Once we know about the 3 different parts (left, middle, right) of the traversals, we can recursively solve the same problem on the original tree’s left subtree and right subtree. A (somewhat Pythonic) pseudocode would be:
def buildTree(inorder, postorder):
# stop condition(s) for recursion
if len(inorder) == 0 and len(postorder) == 0:
return null
(# optional optimization for leaves
if len(inorder) == 1 and len(postorder) == 1:
Tree.middle = inorder[0] or postorder[0]
return Tree)
# find middle
middle = postorder[-1]
# find left
inorder_left = ...
postorder_left = ...
# find right
inorder_right = ...
postorder_right = ...
# recursion
Tree.middle = middle
Tree.left = buildTree(inorder_left, postorder_left)
Tree.right = buildTree(inorder_right, postorder_right)
return Tree
Implementation details
Although the general idea might be clear, there are a lot of pitholes when implementing the algorithm. One easy pithole to fall in is to not have the same closure criteria when finding the left and right subtrees. It does not matter which closure criteria to use out of these: open-open (), open-close (], close-open [), close-close[], one must be consistent across the implementation. Assuming we use the close-close[] closure, and array[a, b] signifies the slice of the array from index a to index b inclusive, we have as pseudocode:
# finding middle
middle_value = postorder[-1]
for index, value in enumerate(inorder):
if value == middle_value:
middle_index = index
break
# finding left
inorder_left = inorder[0, middle_index - 1]
postorder_left = postorder[0, middle_index - 1] # no matter the traversal, left subtree has same number of elements
# finding right
inorder_right = inorder[middle_index + 1, len(inorder) - 1]
postorder_right = postorder[middle_index, len(postorder) - 2] # here last item is middle, so we exclude it
Below is a fully working Java implementation. As Java does not have built-in array slicing like Python does, we need start and end indexes to delimit the arrays:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return builderTreeHelper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
}
private TreeNode builderTreeHelper(int[] inorder, int startIdxInorder, int endIdxInorder, int[] postorder, int startIdxPostorder, int endIdxPostorder) {
if(endIdxInorder < startIdxInorder) return null;
if(endIdxInorder == startIdxInorder) return new TreeNode(inorder[endIdxInorder]);
int middle = postorder[endIdxPostorder];
TreeNode construct = new TreeNode(middle);
int middleIdx = startIdxInorder;
while(middleIdx <= endIdxInorder) {
if(middle == inorder[middleIdx]) break;
middleIdx++;
}
int startIdxInorderL = startIdxInorder;
int endIdxInorderL = middleIdx - 1;
int startIdxInorderR = middleIdx + 1;
int endIdxInorderR = endIdxInorder;
int startIdxPostorderL = startIdxPostorder;
int endIdxPostorderL = middleIdx - startIdxInorder + startIdxPostorder - 1;
int startIdxPostorderR = middleIdx - startIdxInorder + startIdxPostorder;
int endIdxPostorderR = endIdxPostorder - 1;
construct.left = builderTreeHelper(inorder, startIdxInorderL, endIdxInorderL, postorder, startIdxPostorderL, endIdxPostorderL);
construct.right = builderTreeHelper(inorder, startIdxInorderR, endIdxInorderR, postorder, startIdxPostorderR, endIdxPostorderR);
return construct;
}
}Comparison with levelorder traversal
If we have a levelorder array, it is already enough to build the tree. In which we have:
parent_idx = n
left_child_idx = 2n + 1 # n starts from 0
(left_child_idx = 2n # n starts from 1)
right_child_idx = 2n + 2 # n starts from 0
(right_child_idx = 2n + 1 # n starts from 1)
However, we need nulls to be put inside the array for the above to work. With preorder/postorder and inorder arrays, we would be able to construct the tree without null values. It is a memory vs computation tradeoff.